Поиск ранга матрицы. Вычисление ранга матрицы с помощью элементарных преобразований

Строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы - наивысший из порядков всевозможных ненулевых миноров этой матрицы. Ранг нулевой матрицы любого размера ноль. Если все миноры второго порядка равны нулю, то ранг равен единице, и т.д.

Ранг матрицы - размерность образа dim ⁡ (im ⁡ (A)) {\displaystyle \dim(\operatorname {im} (A))} линейного оператора , которому соответствует матрица.

Обычно ранг матрицы A {\displaystyle A} обозначается rang ⁡ A {\displaystyle \operatorname {rang} A} , r ⁡ A {\displaystyle \operatorname {r} A} , rg ⁡ A {\displaystyle \operatorname {rg} A} или rank ⁡ A {\displaystyle \operatorname {rank} A} . Последний вариант свойственен для английского языка, в то время как первые два - для немецкого, французского и ряда других языков.

Энциклопедичный YouTube

• 1 / 5

  Пусть - прямоугольная матрица.

  Тогда по определению рангом матрицы A {\displaystyle A} является:

  Теорема (о корректности определения рангов). Пусть все миноры матрицы A m × n {\displaystyle A_{m\times n}} порядка k {\displaystyle k} равны нулю ( M k = 0 {\displaystyle M_{k}=0} ). Тогда ∀ M k + 1 = 0 {\displaystyle \forall M_{k+1}=0} , если они существуют.

  Связанные определения

  Свойства

  • Теорема (о базисном миноре): Пусть r = rang ⁡ A , M r {\displaystyle r=\operatorname {rang} A,M_{r}} - базисный минор матрицы A {\displaystyle A} , тогда:
  • Следствия:
  • Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями . Тогда справедливо утверждение: Если A ∼ B {\displaystyle A\sim B} , то их ранги равны.
  • Теорема Кронекера - Капелли : Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
    • Количество главных переменных системы равно рангу системы.
    • Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
  • Неравенство Сильвестра : Если A и B матрицы размеров m x n и n x k , то
  rang ⁡ A B ≥ rang ⁡ A + rang ⁡ B − n {\displaystyle \operatorname {rang} AB\geq \operatorname {rang} A+\operatorname {rang} B-n}

  Это частный случай следующего неравенства.

  • Неравенство Фробениуса : Если AB, BC, ABC корректно определены, то
  rang ⁡ A B C ≥ rang ⁡ A B + rang ⁡ B C − rang ⁡ B {\displaystyle \operatorname {rang} ABC\geq \operatorname {rang} AB+\operatorname {rang} BC-\operatorname {rang} B}

  Линейное преобразование и ранг матрицы

  Пусть A {\displaystyle A} - матрица размера m × n {\displaystyle m\times n} над полем C {\displaystyle C} (или R {\displaystyle R} ). Пусть T {\displaystyle T} - линейное преобразование, соответствующее A {\displaystyle A} в стандартном базисе; это значит, что T (x) = A x {\displaystyle T(x)=Ax} . Ранг матрицы A {\displaystyle A} - это размерность области значений преобразования T {\displaystyle T} .

  Методы

  Существует несколько методов нахождения ранга матрицы:

  • Метод элементарных преобразований
  Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
  • Метод окаймляющих миноров
  Пусть в матрице A {\displaystyle A} найден ненулевой минор k {\displaystyle k} -го порядка M {\displaystyle M} . Рассмотрим все миноры (k + 1) {\displaystyle (k+1)} -го порядка, включающие в себя (окаймляющие) минор M {\displaystyle M} ; если все они равны нулю, то ранг матрицы равен k {\displaystyle k} . В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

  Ранее для квадратной матрицы -го порядка было введено понятие минора
  элемента. Напомним, что так был назван определитель порядка
  , полученный из определителя
  вычеркиванием-й строки и-го столбца.

  Введем теперь общее понятие минора. Рассмотрим некоторую, не обязательно квадратную матрицу . Выберем какие-нибудьномеров строк
  иномеров столбцов
  .

  Определение . Минором порядка матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка, образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число

  .

  Каждая матрица имеет столько миноров данного порядка , сколькими способами можно выбрать номера строк
  и столбцов
  .

  Определение . В матрице размеров
  минор порядканазываетсябазисным , если он отличен от нуля, а все миноры порядка
  равны нулю или миноров порядка
  у матрицывообще нет.

  Ясно, что в матрице может быть несколько разных базисных миноров, но все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка
  равны нулю, то равны нулю и все миноры порядка
  , а, следовательно, и всех бόльших порядков.

  Определение . Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.

  Ранг матрицы будем обозначать символом
  . Из определения ранга следует, что для матрицыразмеров
  справедливо соотношение.

  Два способа вычисления ранга матрицы

  а) Метод окаймляющих миноров

  Пусть в матрице найден минор
  -го порядка, отличный от нуля. Рассмотрим лишь те миноры
  -го порядка, которые содержат в себе (окаймляют) минор
  : если все они равны нулю, то ранг матрицы равен. В противном случае среди окаймляющих миноров найдется ненулевой минор
  -го порядка, и вся процедура повторяется.

  Пример 9 . Найти ранг матрицы методом окаймляющих миноров.

  

  Выберем минор второго порядка
  . Существует только один минор третьего порядка, окаймляющий выбранный минор
  . Вычислим его.

  

  Значит, минор
  базисный, а ранг матрицы равен его порядку, т.е.
  

  Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.

  б) Метод элементарных преобразований

  Определение . Элементарными преобразованиями матрицы называют следующие преобразования:

  умножение строки на число, отличное от нуля;

  прибавление к одной строке другой строки;

  перестановку строк;

  такие же преобразования столбцов.

  Преобразования 1 и 2 выполняются поэлементно.

  Комбинируя преобразования первого и второго вида, мы можем к любой строке прибавить линейную комбинацию остальных строк.

  Теорема . Элементарные преобразования не меняют ранга матрицы.

  (Без доказательства)

  Идея практического метода вычисления ранга матрицы

  

  заключается в том, что с помощью элементарных преобразований данную матрицу приводят к виду

  , (5)

  в котором «диагональные» элементы
  отличны от нуля, а элементы, расположенные ниже «диагональных», равны нулю. Условимся называть матрицутакого вида треугольной (иначе, ее называют диагональной, трапециевидной или лестничной). После приведения матрицык треугольному виду можно сразу записать, что
  .

  В самом деле,
  (т.к. элементарные преобразования не меняют ранга). Но у матрицысуществует отличный от нуля минор порядка:

  ,

  а любой минор порядка
  содержит нулевую строку и поэтому равен нулю.

  Сформулируем теперь практическое правило вычисления ранга матрицы с помощью элементарных преобразований: для нахождения ранга матрицыследует с помощью элементарных преобразований привести ее к треугольному виду. Тогда ранг матрицыбудет равен числу ненулевых строк в полученной матрице.

  Пример 10. Найти ранг матрицы методом элементарных преобразований

  

  Решение.

  Поменяем местами первую и вторую строку (т.к. первый элемент второй строки −1 и с ней будет удобно выполнять преобразования). В результате получим матрицу, эквивалентную данной.

  
  

  Обозначим -тую строку матрицы –. Нам необходимо привести исходную матрицу к треугольному виду. Первую строку будем считать ведущей, она будет участвовать во всех преобразованиях, но сама остается без изменений.

  На первом этапе выполним преобразования, позволяющие получить в первом столбце нули, кроме первого элемента. Для этого из второй строки вычтем первую, умноженную на 2
  , к третьей строке прибавим первую
  , а из третьей вычтем первую, умноженную на 3
  Получаем матрицу, ранг которой совпадает с рангом данной матрицы. Обозначим ее той же буквой:

  .

  Так как нам необходимо привести матрицу к виду (5), вычтем из четвертой строки вторую. При этом имеем:

  .

  Получена матрица треугольного вида, и можно сделать вывод, что
  , т. е. числу ненулевых строк. Коротко решение задачи можно записать следующим образом:

  
  

  А также рассмотрим важное практическое приложение темы: исследование системы линейных уравнений на совместность .

  Что такое ранг матрицы?

  В юмористическом эпиграфе статьи содержится большая доля истины. Само слово «ранг» у нас обычно ассоциируется с некоторой иерархией, чаще всего, со служебной лестницей. Чем больше у человека знаний, опыта, способностей, блата и т.д. – тем выше его должность и спектр возможностей. Выражаясь по молодёжному, под рангом подразумевают общую степень «крутизны».

  И братья наши математические живут по тем же принципам. Выведем на прогулку несколько произвольных нулевых матриц :
  

  Задумаемся, если в матрице одни нули , то о каком ранге может идти речь? Всем знакомо неформальное выражение «полный ноль». В обществе матриц всё точно так же:

  Ранг нулевой матрицы любых размеров равен нулю .

  Примечание : нулевая матрица обозначается греческой буквой «тета»

  В целях лучшего понимания ранга матрицы здесь и далее я буду привлекать на помощь материалы аналитической геометрии . Рассмотрим нулевой вектор нашего трёхмерного пространства, который не задаёт определённого направления и бесполезен для построения аффинного базиса . С алгебраической точки зрения координаты данного вектора записаны в матрицу «один на три» и логично (в указанном геометрическом смысле) считать, что ранг этой матрицы равен нулю.

  Теперь рассмотрим несколько ненулевых векторов-столбцов и векторов-строк :
  
  
  В каждом экземпляре есть хотя бы один ненулевой элемент, и это уже кое-что!

  Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице

  И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы .

  Алгебраические векторы-строки и векторы-столбцы в известной степени абстрактны, поэтому снова обратимся к геометрической ассоциации. Ненулевой вектор задаёт вполне определённое направление в пространстве и годится для построения базиса , поэтому ранг матрицы будем считать равным единице.

  Теоретическая справка : в линейной алгебре вектор – это элемент векторного пространства (определяемое через 8 аксиом), который, в частности, может представлять собой упорядоченную строку (или столбец) действительных чисел с определёнными для них операциями сложения и умножения на действительное число. С более подробной информацией о векторах можно ознакомиться в статье Линейные преобразования .

  линейно зависимы (выражаются друг через друга). С геометрической точки зрения во вторую строку записаны координаты коллинеарного вектора , который ничуть не продвинул дело в построении трёхмерного базиса , являясь в этом смысле лишним. Таким образом, ранг данной матрицы тоже равен единице.

  Перепишем координаты векторов в столбцы (транспонируем матрицу ):
  

  Что изменилось с точки зрения ранга? Ничего. Столбцы пропорциональны, значит, ранг равен единице. Кстати, обратите внимание, что все три строки тоже пропорциональны. Их можно отождествить с координатами трёх коллинеарных векторов плоскости, из которых только один полезен для построения «плоского» базиса. И это полностью согласуется с нашим геометрическим смыслом ранга.

  Из вышеприведённого примера следует важное утверждение:

  Ранг матрицы по строкам равен рангу матрицы по столбцам . Об этом я уже немного упоминал на уроке об эффективных методах вычисления определителя .

  Примечание : из линейной зависимости строк следует линейная зависимость столбцов (и наоборот). Но в целях экономии времени, да и в силу привычки я почти всегда буду говорить о линейной зависимости строк.

  Продолжим дрессировать нашего любимого питомца. Добавим в матрицу третьей строкой координаты ещё одного коллинеарного вектора :
  

  Помог ли он нам в построении трёхмерного базиса? Конечно, нет. Все три вектора гуляют туда-сюда по одной дорожке, и ранг матрицы равен единице. Можно взять сколько угодно коллинеарных векторов, скажем, 100, уложить их координаты в матрицу «сто на три» и ранг такого небоскрёба всё равно останется единичным.

  Познакомимся с матрицей , строки которой линейно независимы . Пара неколлинеарных векторов пригодна для построения трёхмерного базиса. Ранг этой матрицы равен двум.

  А чему равен ранг матрицы ? Строки вроде не пропорциональны…, значит, по идее трём. Однако ранг этой матрицы тоже равен двум. Я сложил первые две строки и записал результат внизу, то есть линейно выразил третью строку через первые две. Геометрически строки матрицы соответствуют координатам трёх компланарных векторов , причём среди этой тройки существует пара неколлинеарных товарищей.

  Как видите, линейная зависимость в рассмотренной матрице не очевидна, и сегодня мы как раз научимся выводить её «на чистую воду».

  Думаю, многие догадываются, что такое ранг матрицы!

  Рассмотрим матрицу , строки которой линейно независимы . Векторы образуют аффинный базис , и ранг данной матрицы равняется трём.

  Как вы знаете, любой четвёртый, пятый, десятый вектор трёхмерного пространства будет линейно выражаться через базисные векторы. Поэтому, если в матрицу добавить любое количество строк, то её ранг всё равно будет равен трём .

  Аналогичные рассуждения можно провести для матриц бОльших размеров (понятно, уже без геометрического смысла).

  Определение : ранг матрицы – это максимальное количество линейно независимых строк . Или: ранг матрицы – это максимальное количество линейно независимых столбцов . Да, их количество всегда совпадает.

  Из вышесказанного также следует важный практический ориентир: ранг матрицы не превосходит её минимальной размерности . Например, в матрице четыре строки и пять столбцов. Минимальная размерность – четыре, следовательно, ранг данной матрицы заведомо не превзойдёт 4.

  Обозначения : в мировой теории и практике не существует общепринятого стандарта для обозначения ранга матрицы, наиболее часто можно встретить: – как говорится, англичанин пишет одно, немец другое. Поэтому давайте по мотивам известного анекдота про американский и русский ад обозначать ранг матрицы родным словом. Например: . А если матрица «безымянная», коих встречается очень много, то можно просто записать .

  Как найти ранг матрицы с помощью миноров?

  Если бы у бабушки нас в матрице был пятый столбец, то следовало бы вычислить ещё один минор 4-го порядка («синие», «малиновый» + 5-й столбец).

  Вывод : максимальный порядок ненулевого минора равен трём, значит, .

  Возможно, не все до конца осмыслили данную фразу: минор 4-го порядка равен нулю, но среди миноров 3-го порядка нашёлся ненулевой – поэтому максимальный порядок ненулевого минора и равен трём.

  Возникает вопрос, а почему бы сразу не вычислить определитель? Ну, во-первых, в большинстве заданий матрица не квадратная, а во-вторых, даже если у вас и получится ненулевое значение, то задание с высокой вероятностью забракуют, так как оно обычно подразумевает стандартное решение «снизу вверх». А в рассмотренном примере нулевой определитель 4-го порядка и вовсе позволяет утверждать, что ранг матрицы лишь меньше четырёх.

  Должен признаться, разобранную задачу я придумал сам, чтобы качественнее объяснить метод окаймляющих миноров. В реальной практике всё проще:

  Пример 2

  Найти ранг матрицы методом окаймляющих миноров
  

  Решение и ответ в конце урока.

  Когда алгоритм работает быстрее всего? Вернёмся к той же матрице «четыре на четыре» . Очевидно, решение будет самым коротким в случае «хороших» угловых миноров :
  

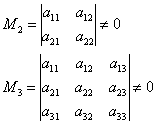
  И, если , то , в противном случае – .

  Размышление совсем не гипотетично – существует немало примеров, где всё дело и ограничивается только угловыми минорами.

  Однако в ряде случаев более эффективен и предпочтителен другой способ:

  Как найти ранг матрицы с помощью метода Гаусса?

  Параграф рассчитан на читателей, которые уже знакомы с методом Гаусса и мало-мальски набили на нём руку.

  С технической точки зрения метод не отличается новизной:

  1) с помощью элементарных преобразований приводим матрицу к ступенчатому виду;

  2) ранг матрицы равен количеству строк.

  Совершенно понятно, что использование метода Гаусса не меняет ранга матрицы , и суть здесь предельно проста: согласно алгоритму, в ходе элементарных преобразований выявляются и удаляются все лишние пропорциональные (линейно зависимые) строки, в результате чего остаётся «сухой остаток» – максимальное количество линейно независимых строк.

  Преобразуем старую знакомую матрицу с координатами трёх коллинеарных векторов:
  

  (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку.

  (2) Нулевые строки удаляем.

  Таким образом, осталась одна строка, следовательно, . Что и говорить, это гораздо быстрее, чем рассчитать девять нулевых миноров 2-го порядка и только потом сделать вывод.

  Напоминаю, что в самой по себе алгебраической матрице ничего менять нельзя, и преобразования выполняются только с целью выяснения ранга! Кстати, остановимся ещё раз на вопросе, почему нельзя? Исходная матрица 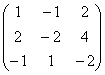несёт информацию, которая принципиально отлична от информации матрицы и строки . В некоторых математических моделях (без преувеличения) разница в одном числе может быть вопросом жизни и смерти. …Вспомнились школьные учителя математики начальных и средних классов, которые безжалостно срезали оценку на 1-2 балла за малейшую неточность или отклонение от алгоритма. И было жутко обидно, когда вместо, казалось бы, гарантированной «пятёрки» получалось «хорошо» или того хуже. Понимание пришло намного позже – а как иначе доверить человеку спутники, ядерные боеголовки и электростанции? Но вы не беспокойтесь, я не работаю в этих сферах =)

  Перейдём к более содержательным заданиям, где помимо прочего познакомимся с важными вычислительными приёмами метода Гаусса :

  Пример 3

  Найти ранг матрицы с помощью элементарных преобразований
  

  Решение : дана матрица «четыре на пять», значит, её ранг заведомо не больше, чем 4.

  В первом столбце, отсутствует 1 или –1, следовательно, необходимы дополнительные действия, направленные на получение хотя бы одной единицы. За всё время существования сайта мне неоднократно задавали вопрос: «Можно ли в ходе элементарных преобразований переставлять столбцы?». Вот здесь – переставили первый-второй столбец, и всё отлично! В большинстве задач, где используется метод Гаусса , столбцы действительно переставлять можно. НО НЕ НУЖНО. И дело даже не в возможной путанице с переменными, дело в том, что в классическом курсе обучения высшей математике данное действие традиционно не рассматривается, поэтому на такой реверанс посмотрят ОЧЕНЬ криво (а то и заставят всё переделывать).

  Второй момент касается чисел. В ходе решения полезно руководствоваться следующим эмпирическим правилом: элементарные преобразования по возможности должны уменьшать числа матрицы . Ведь с единицей-двойкой-тройкой работать значительно легче, чем, например, с 23, 45 и 97. И первое действие направлено не только на получение единицы в первом столбце, но и на ликвидацию чисел 7 и 11.

  Сначала полное решение, потом комментарии:
  
  

  (1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3. И до кучи: к 4-й строке прибавили 1-ю строку, умноженную на –1.

  (2) Последние три строки пропорциональны. Удалили 3-ю и 4-ю строки, вторую строку переместили на первое место.

  (3) Ко второй строке прибавили первую строку, умноженную на –3.

  В приведённой к ступенчатому виду матрице две строки.

  Ответ :

  Теперь ваша очередь мучить матрицу «четыре на четыре»:

  Пример 4

  Найти ранг матрицы методом Гаусса
  

  Напоминаю, что метод Гаусса не предполагает однозначной жёсткости, и ваше решение, скорее всего, будет отличаться от моего решения. Краткий образец оформления задачи в конце урока.

  Какой метод использовать для нахождения ранга матрицы?

  На практике зачастую вообще не сказано, какой метод необходимо использовать для нахождения ранга. В такой ситуации следует анализировать условие – для одних матриц рациональнее провести решение через миноры, а для других значительно выгоднее применить элементарные преобразования:

  Пример 5

  Найти ранг матрицы
  

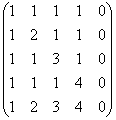
  Решение : первый способ как-то сразу отпадает =)

  Чуть выше я советовал не трогать столбцы матрицы, но когда есть нулевой столбец, либо пропорциональные/совпадающие столбцы, то всё же стОит провести ампутацию:
  
  

  (1) Пятый столбец нулевой, удалим его из матрицы. Таким образом, ранг матрицы не больше четырёх. Первую строку умножили на –1. Это ещё одна фирменная фишка метода Гаусса, превращающая следующее действие в приятную прогулку:

  (2) Ко всем строкам, начиная со второй, прибавили первую строку.

  (3) Первую строку умножили на –1, третью строку разделили на 2, четвёртую строку разделили на 3. К пятой строке прибавили вторую строку, умноженную на –1.

  (4) К пятой строке прибавили третью строку, умноженную на –2.

  (5) Последние две строки пропорциональны, пятую удаляем.

  В результате получено 4 строки.

  Ответ :

  Стандартная пятиэтажка для самостоятельного исследования:

  Пример 6

  Найти ранг матрицы
  

  Краткое решение и ответ в конце урока.

  Следует отметить, что словосочетание «ранг матрицы» не так часто встретишь на практике, и в большинстве задач можно вообще обойтись без него. Но существует одно задание, где рассматриваемое понятие является главным действующим лицом, и в заключение статьи мы рассмотрим это практическое приложение:

  Как исследовать систему линейных уравнений на совместность?

  Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли , которую я сформулирую в необходимом виде:

  Если ранг матрицы системы равен рангу расширенной матрицы системы , то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.

  Таким образом, для исследования системы на совместность нужно проверить равенство 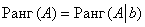, где – матрица системы (вспоминаем терминологию из урока Метод Гаусса ), а – расширенная матрица системы (т.е. матрица с коэффициентами при переменных + столбец свободных членов).

  Пусть задана некоторая матрица :

  .

  Выделим в этой матрице произвольных строк ипроизвольных столбцов
  . Тогда определитель-го порядка, составленный из элементов матрицы
  , расположенных на пересечении выделенных строк и столбцов, называется минором-го порядка матрицы
  .

  Определение 1.13. Рангом матрицы
  называется наибольший порядок минора этой матрицы, отличного от нуля.

  Для вычисления ранга матрицы следует рассматривать все ее миноры наименьшего порядка и, если хоть один из них отличный от нуля, переходить к рассмотрению миноров старшего порядка. Такой подход к определению ранга матрицы называется методом окаймления (или методом окаймляющих миноров).

  Задача 1.4. Методом окаймляющих миноров определить ранг матрицы
  .

  .

  Рассмотрим окаймление первого порядка, например,
  . Затем перейдем к рассмотрению некоторого окаймления второго порядка.

  Например,
  .

  Наконец, проанализируем окаймление третьего порядка.

  .

  Таким образом, наивысший порядок минора, отличного от нуля, равен 2, следовательно,
  .

  При решении задачи 1.4 можно заметить, что ряд окаймляющих миноров второго порядка отличны от нуля. В этой связи имеет место следующее понятие.

  Определение 1.14. Базисным минором матрицы называется всякий, отличный от нуля минор, порядок которого равен рангу матрицы.

  Теорема 1.2. (Теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы.

  Заметим, что строки (столбцы) матрицы линейно зависимы тогда и только тогда, когда хотя бы одну из них можно представить как линейную комбинацию остальных.

  Теорема 1.3. Число линейно независимых строк матрицы равно числу линейно независимых столбцов матрицы и равно рангу матрицы.

  Теорема 1.4. (Необходимое и достаточное условие равенства нулю определителя). Для того, чтобы определитель-го порядкабыл равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.

  Вычисление ранга матрицы, основанное на использовании его определения, является слишком громоздкой операцией. Особенно это становится существенным для матриц высоких порядков. В этой связи на практике ранг матрицы вычисляют на основании применения теорем 10.2 - 10.4, а также использования понятий эквивалентности матриц и элементарных преобразований.

  Определение 1.15. Две матрицы
  иназываются эквивалентными, если их ранги равны, т.е.
  .

  Если матрицы
  иэквивалентны, то отмечают
  .

  Теорема 1.5. Ранг матрицы не меняется от элементарных преобразований.

  Будем называть элементарными преобразованиями матрицы
  любые из следующих действий над матрицей:

  Замену строк столбцами, а столбцов соответствующими строками;

  Перестановку строк матрицы;

  Вычеркивание строки, все элементы которой равны нулю;

  Умножение какой-либо строки на число, отличное от нуля;

  Прибавление к элементам одной строки соответствующих элементов другой строки умноженных на одно и то же число
  .

  Следствие теоремы 1.5. Если матрица
  получена из матрицыпри помощи конечного числа элементарных преобразований, то матрицы
  иэквивалентны.

  При вычислении ранга матрицы ее следует привести при помощи конечного числа элементарных преобразований к трапециевидной форме.

  Определение 1.16. Трапециевидной будем называть такую форму представления матрицы, когда в окаймляющем миноре наибольшего порядка отличного от нуля все элементы, стоящие ниже диагональных, обращаются в нуль. Например:

  .

  

  Здесь
  , элементы матрицы
  обращаются в нуль. Тогда форма представления такой матрицы будет трапециевидной.

  Как правило, матрицы к трапециевидной форме приводят при помощи алгоритма Гаусса. Идея алгоритма Гаусса состоит в том, что, умножая элементы первой строки матрицы на соответствующие множители, добиваются, чтобы все элементы первого столбца, расположенные ниже элемента
  , превращались бы в нуль. Затем, умножая элементы второго столбца на соответствующие множители, добиваются, чтобы все элементы второго столбца, расположенные ниже элемента
  , превращались бы в нуль. Далее поступают аналогично.

  Задача 1.5. Определить ранг матрицы путем сведения ее к трапециевидной форме.

  .

  Для удобства применения алгоритма Гаусса можно поменять местами первую и третью строки.

  
  
  

  
  
  
  .

  Очевидно, что здесь
  . Однако, для приведения результата к более изящному виду можно далее продолжить преобразования над столбцами.

  
  
  
  

  
  
  
  
  .

  Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r , то это означает, что в матрице А имеется отличный от нуля минор порядка r , но всякий минор порядка, большего чем r , равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

  Вычисление ранга матрицы с помощью миноров

  Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k .

  Пример 1. Найти методом окаймления миноров ранг матрицы

  .

  Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М 1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M 2 = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2 . Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

  Вычисление ранга матрицы с помощью элементарных преобразований

  Элементарными называются следующие преобразования матрицы:

  1) перестановка двух любых строк (или столбцов),

  2) умножение строки (или столбца) на отличное от нуля число,

  3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

  Две матрицы называются эквивалентными , если одна из них получается из другой с помощью конечного множества элементарных преобразований.

  Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

  Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

  .

  При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

  Пример 2 Найти ранг матрицы

  

  и привести ее к каноническому виду.

  Решение. Из второй строки вычтем первую и переставим эти строки:

  .

  Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

  ;

  из третьей строки вычтем первую; получим матрицу

  

  которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

  .